I: Data problems (and solution concepts) in ML

Suppose you wanted to train an ML model. Even after deciding on the best training recipe to use, and securing enough compute to train the model, you’ll have to answer questions like:

What types of data should I train my model on?
How much should I pay for different providers’ data?
Can I get away with using less data, and if so how?

Then, after you train your model, you’ll observe its behavior, and have more questions:

Which training data points were responsible for this unwanted behavior?
How sensitive is my model to maliciously inserted training data?
When can I trust that the outputs of my model are grounded in real facts?
Where do I need to collect more data?

What all of these questions have in common is that they are “data questions.” They require us to relate the output of machine learning models (whether it’s performance, specific predictions, or general behaviors) to the data that we train them on. The general class of methods for answering these questions is called data attribution.

The goal of this chapter—and more broadly, this tutorial—is to survey the large (and growing) field of data attribution. Our goals will be to:

Illustrate the many distinct perspectives on data attribution, each defined by a different formalization of the (initially vague) task of “connecting model behavior and training data.”
Highlight connections between these perspectives and existing well-established frameworks in fields such as statistics, information retrieval, and game theory.
Discuss challenges in scaling data attribution methods (broadly construed) to the large models and datasets of modern ML.

In this chapter, we’re going to talk about three different perspectives (or solution concepts), based on three different conceptions of the data attribution problem. In the coming chapters, we are going to focus in on a specific one of these solution concepts.

Three notions of data attribution

Broadly, a data attribution method is a tool for relating the output of a machine learning model to the data that the model trained on. This goal, however, is quite vague—how exactly we choose to formalize it, and the exact desiderata we ask for, will determine what type of data attribution we are actually after.

Through the rest of the section, we’ll assume we have the following:

A universe of data $\mathcal{U}$ (think all possible documents, or all possible images; but often we will fix $\mathcal{U}$ to be finite), from which we can pick datasets $S \subset 2^\mathcal{U}$;
A learning algorithm $\theta(\cdot): 2^{\mathcal{U}} \to \mathcal{M}$ which maps datasets $S$ to machine learning models $M \in \mathcal{M}$ (where $\mathcal{M}$ is the space of all possible ML models);

Generally speaking, once these things are fixed, a data attribution methods aim to relate a dataset $S \in 2^\mathcal{U}$ with some ensuing “measured model behavior” $f(\theta(S))$ (for some function $f$). How exactly we want to relate these two objects defines the type of data attribution method we’re after.

Corroborative attribution (Citation)

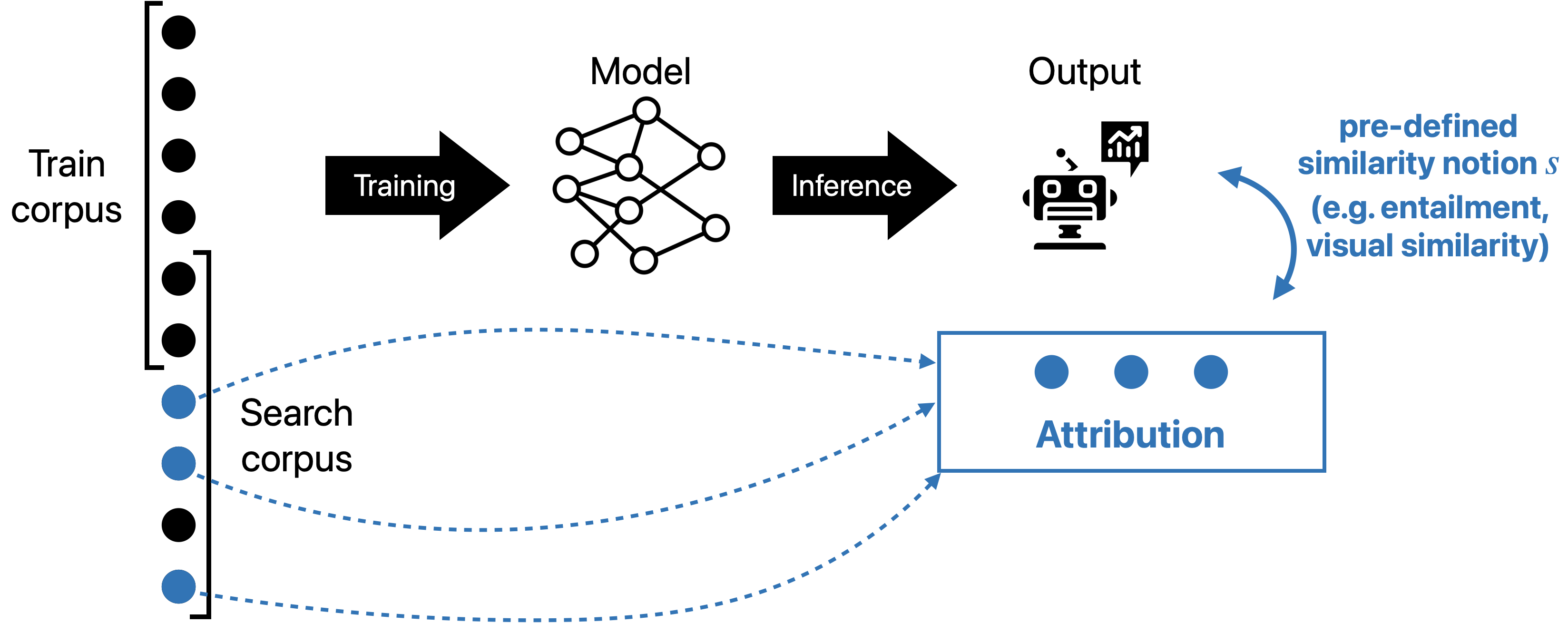
In many applications, we don’t necessarily want to relate model outputs with training data in a causal way—we don’t really care if the model outputted something “because of” a given piece of training data. Take the following two examples:

Example (Citation generation). When a large language model generates an assertion, one popular way of verifying the assertion is by providing citations—examples from the web (or another corpus) that logically entail the assertion.

Example (Copyright infringement). When judging whether art generated by a generative AI model is “original,” we might be interested in finding the nearest neighbors to that image from a corpus of publicly available art on the internet.

Notably, in these two applications, the examples that we surface do not have to have caused the ML model to behave a certain way—indeed, they need not even be in the training data! Just the existence of data that in some way “look like” the model prediction is enough. These applications motivate a solution concept that Worledge et al. [WSM+23] call corroborative attribution.

Problem Statement (Corroborative attribution). Fix the data universe $\,\mathcal{U}$ and algorithm $\theta(\cdot)$ from above. Suppose we have a model trained on a training set $S \subset \mathcal{U}$, and let $S_{targ} \subset \mathcal{U}$. (not necessarily equal to $S$) be an attribution set (e.g., trusted facts, or copyrighted images).

A corroborative attribution method takes as input a model behavior $B$, and as output finds support for the model behavior of interest, i.e., a set of points $\bm{z} \in S_{targ}$ such that $\bm{z} \implies B$ (where $\implies$ is a relation denoting similarity, entailment, support, etc.) .

Examples of corroborative attribution techniques include information retrieval systems and embedding/vector search databases.

Game-theoretic attribution (Credit assignment)

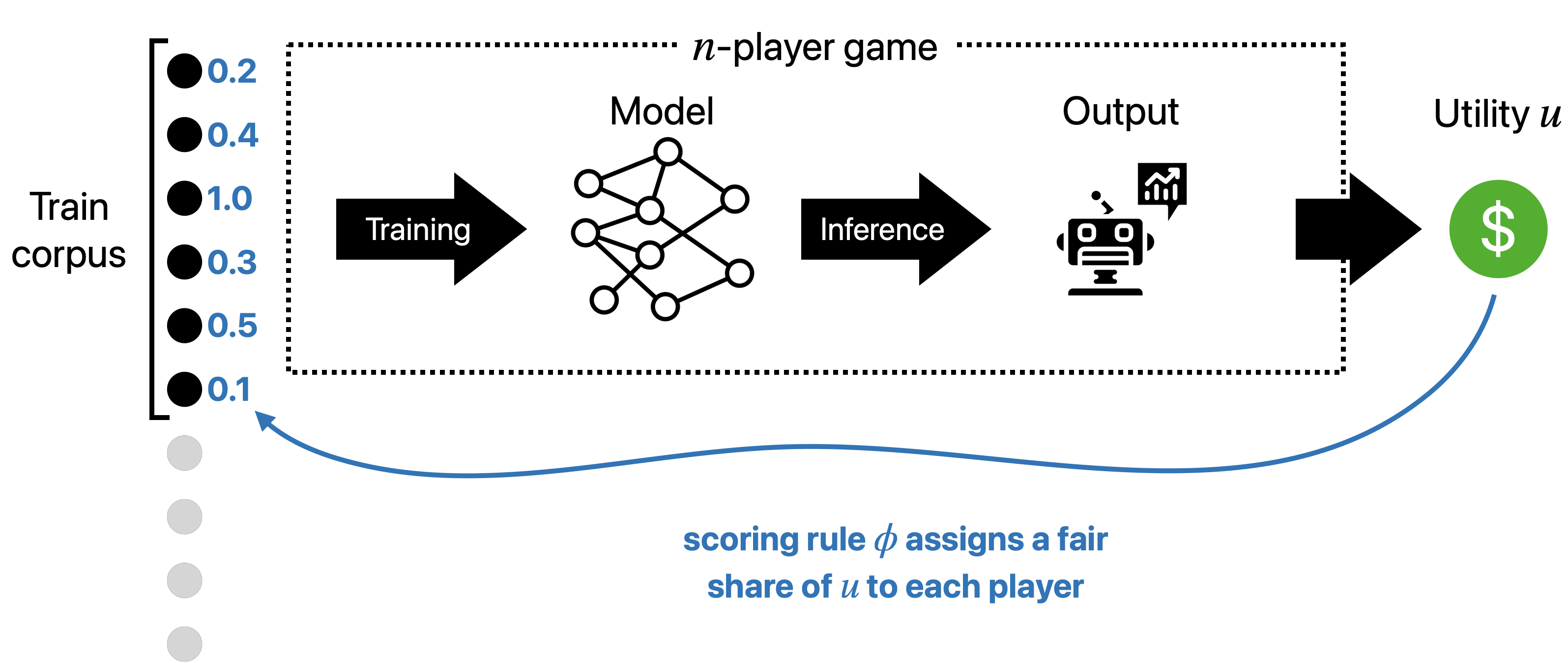
In contrast to corroborative attribution, the next two solution concepts we discuss fall under the umbrella of contributive attribution [WSJ+23], because they actually try to causally link training data to predictions. In this tutorial, we’re actually going to separate contributive attribution into two different types, based on the envisioned downstream use of the attribution method (more on this in Part IV).

Let’s start with what we’ll call the “game-theoretic” solution concept. Here, the focus is on data problems that involve valuing data or assigning responsibility to training data in a “fair” way. To see why this might be useful, consider the following two applications:

Example #1 (Pricing data): Suppose a generative AI model provider wants to compensate artists for generations that are derived from their works. The model provider commits 10% of their profits to such compensation, and wants to give each artist their fair share of the pool.

Example #2: (Passing on liability) Suppose a company sources their data from multiple sources, and something goes wrong—the company would like a way to correctly assign blame across their data sources.

With these examples in mind, let’s try to state a (more) precise problem statement for game-theoretic data attribution:

Problem Statement. Fix the data universe $\,\mathcal{U}$, and algorithm $\theta(\cdot)$ from above. Additionally, let $S \subset \mathcal{U}$ be a fixed training set, and let $M = \theta(S)$ be a model trained on $S$.

A game-theoretic data attribution method takes as input a model utilityA natural way to think about this is profit made from a model $M$, but it can also capture things like the cost incurred by making a given mistake, or even a model's loss on a specific input. $u(M) \in \mathbb{R}$. Treating model training as the outcome of a game with $|S|$ players, game-theoretic data attribution methods assign a fair share of $u$ to each datapoint in $S$ (where "fairness" is determined axiomatically—e.g., we might ask for $v_i = v_j$ if the $i^{\text{th}}$ and $j^{\text{th}}$ training data points are identical).

One example of game-theoretic data attribution mechanisms is the Data Shapley, which assigns values

\[v_i = \sum_{S' \subset S\setminus\lbrace z_i\rbrace} \frac{|S'|!\cdot (|S| - 1 - |S'|)!}{|S|!}\cdot [u(\theta(S' \cup \lbrace z_i\rbrace)) - u(\theta(S'))]\]

This valuation mechanism inherits all the properties of the Shapley value from game theory, meaning that it is the only way to efficiently assign values that are

symmetric (equal datapoints receive equal value),
linear (attributing a linear combination of model behaviors is equivalent to linearly combining individual attributions), and
null-sensitive (datapoints that do not ever affect model behavior receive value zero).

While the Shapley value is the unique valuation function that satisfies these axioms, in general we might care about other axioms, in which case we might want to use a different valuation function.

Predictive attribution (Datamodeling)

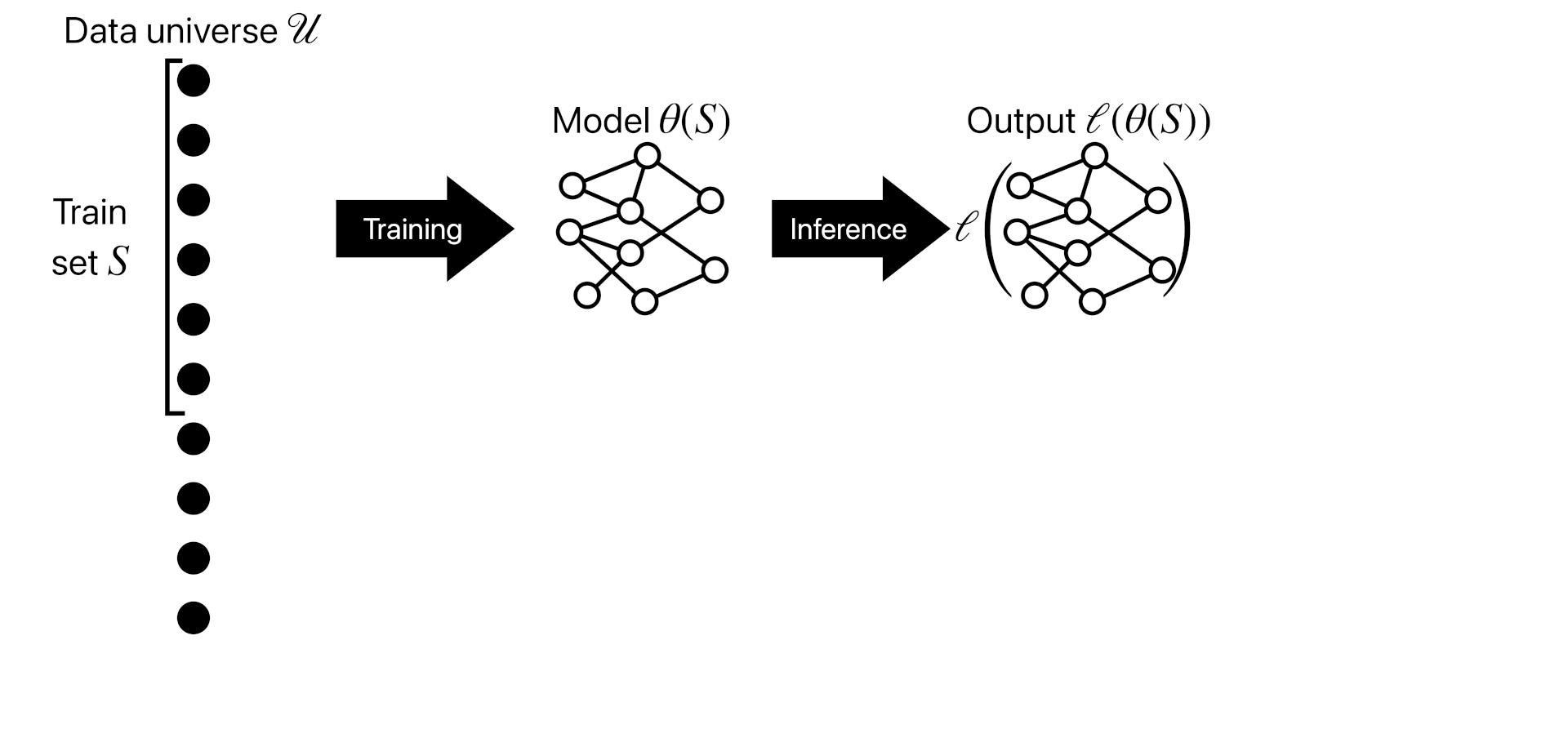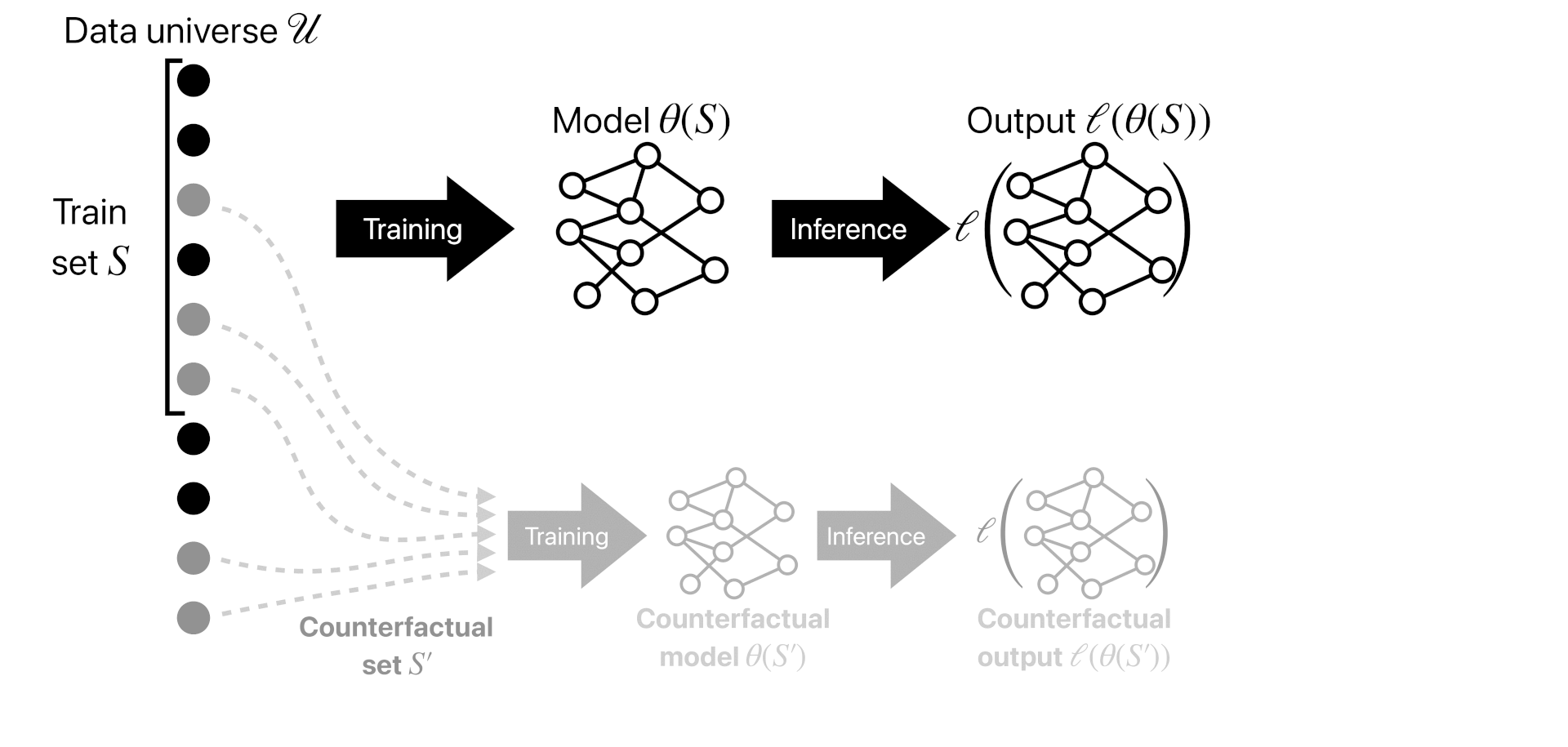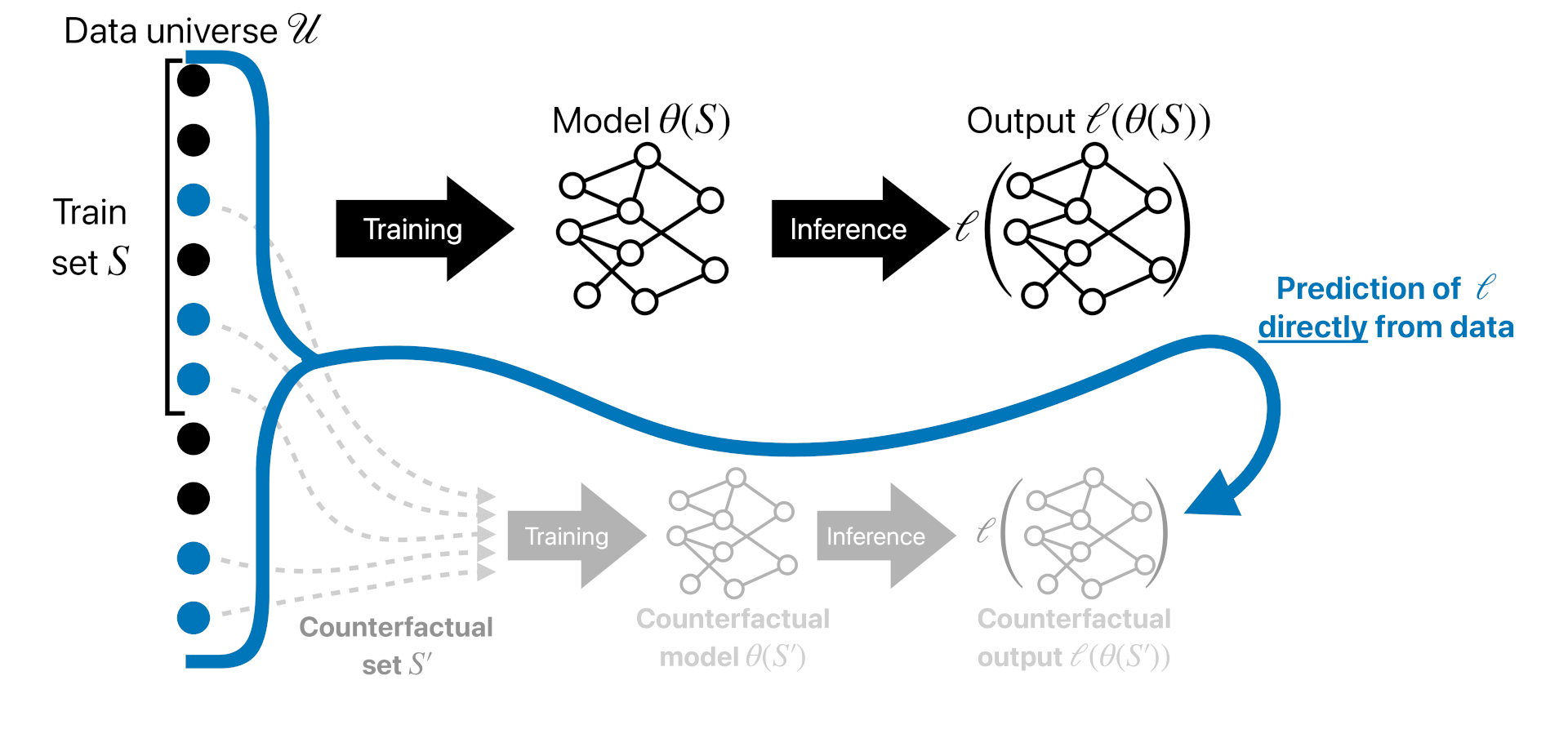
Finally, the focus of this tutorial will be on a third solution concept. Here, the goal is to answer questions of the form “what would have happened has we trained on a different dataset?”

Example #1 (Data selection). Suppose we were training a new model and want to figure out what dataset to train on. What we really want to do is select the dataset that will maximize the performance of the resulting model—to be able to perform this maximization, we need a way of knowing, for a given subset, what the performance of the model will be.

Example #2 (Sensitivity analysis). Predictive data attribution methods also let us answer questions of the form “how many samples would I need to omit in order to flip a statistical conclusion?” Broderick, Giordano and Meager (2020) explore this, e.g., in the context of published economic studies.

Problem Statement. Fix the data universe $\,\mathcal{U}$ and algorithm $\theta(\cdot)$ from above. Additionally, let $\ell: \mathcal{M} \to \mathbb{R}^k$ be an arbitrary measurement functionFor example, $\ell(M)$ might compute the logits of model $M$ on a specific input—or it might compute the per-example loss of model $M$ on a given test set. mapping ML models to real-valued vectors.

The goal of a predictive data attribution method is to output a function $\hat{f}$ (called a datamodel) such that, for any possible training dataset $S \subset \mathcal{U}$, $$\hat{f}(S) \approx \ell(\theta(S)).$$ We also want the datamodel $\hat{f}(S)$ to be much faster to compute than the training algorithm itself (so that $\ell(\theta(\cdot))$ itself is not a valid predictive data attribution method).

Unlike in game-theoretic data attribution, we don’t necessarily care about the internals of how this predictor works—instead, we want it to be:

Fast, so that we can quickly predict how model behavior will change when changing the dataset, without re-training); and
Accurate, so that these predictions are actually reflective of model behavior.

In some cases, we’ll also see that interpretability of the datamodel $\hat{f}$ can be useful—particularly as a tool for interpreting the underlying learning algorithm $\theta(\cdot)$ (more on this later).

How do these different notions of data attribution relate?

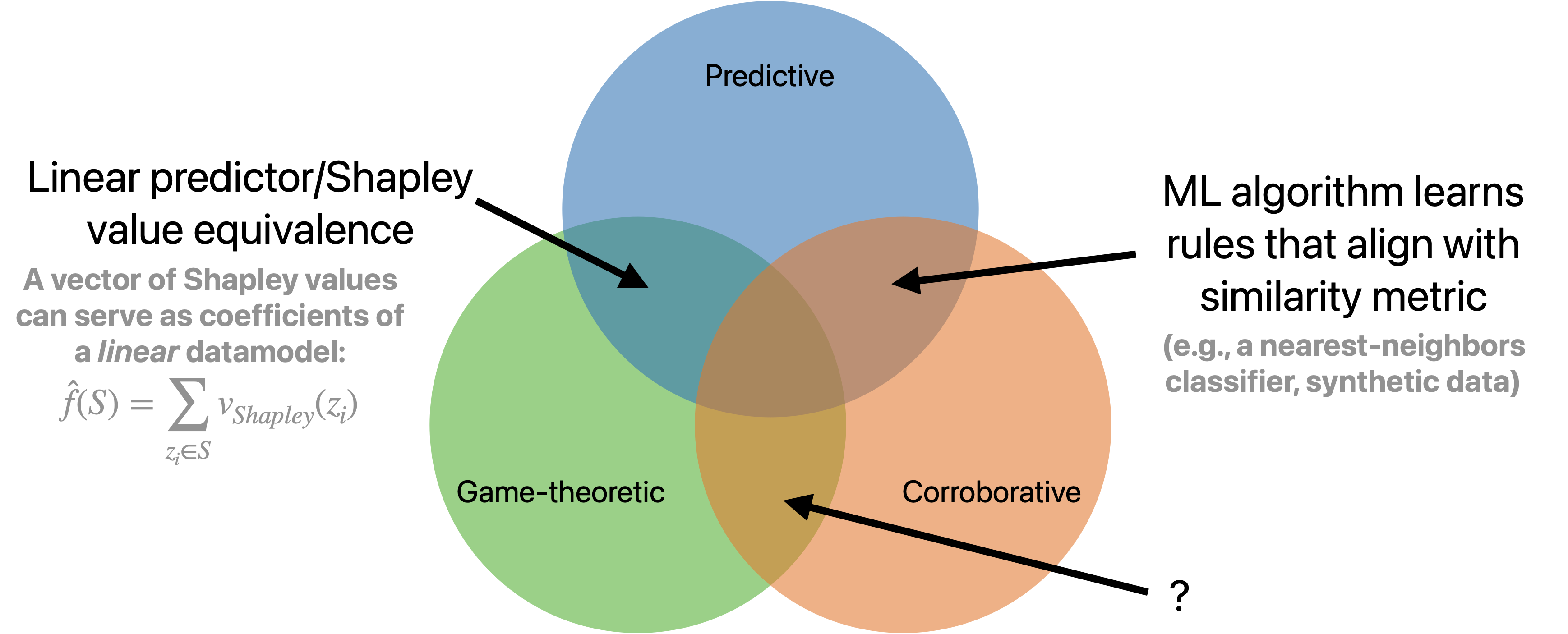
Before moving on, it’s worth reflecting on the precise differences and similarities between the three notions of data attribution we’ve talked about. In particular, we (the authors) want to draw attention to a few facts:

(1) Corroborative importance does not generally imply contributive importance. In general, the fact that a datapoint is surfaced by a corroborative data attribution method says nothing about the datapoint’s impact on the ML model of interest (i.e., what [WSM+23] call its contributive importance). Indeed, we will see in Part III that in computer vision, for example, visual similarity of a training example to a test example (its corroborative importance) is a poor proxy for the effect on the latter of removing the former and re-training (its contributive importance).

(2) Corroborative importance can coincide with contributive importance, for “perfect models.” One situation in which corroborative and contributive attribution do coincide is when the “rules” learned by the training algorithm $\theta(\cdot)$ coincide exactly with the relation being used for corroborative attribution. For example,

For a k-nearest neighbor classifier, a corroborative attribution method based on feature similarity would also be a contributive attribution method.
It is possible to construct synthetic datasets (e.g., this one) which guarantee that corroborative and contributive attribution coincide.

(3) Game-theoretic data attribution methods can also be predictive ones. Finally, there are some conditions under which the two notions of contributive attribution that we’ve discussed (game-theoretic and predictive) coincide. For example, the Shapley value described above has an additional interpretation as a linear datamodel $\smash{\hat{f}}$. In particular, letting $\mathcal{U}$ be the training set, for a training data subset $S \subset \mathcal{U}$, we have that

\[\ell(\theta(S)) \approx \sum_{z_i \in S} v_i,\]

where $v_i$ is the Shapley value assigned to the $i^{\text{th}}$ training data point. (We’ll come back to this linear type of predictive data attribution in Part III.)

In the rest of this tutorial, we will focus specifically on predictive data attribution methods. Up next, we'll discuss the history and theoretical foundations of the predictive attribution problem.

Some links and resources

Below is an incomplete list of resources that talk more about different notions of data attribution:

Theodora Worledge, Judy Hanwen Shen, Nicole Meister, Caleb Winston, Carlos Guestrin. Unifying Corroborative and Contributive Attributions in Large Language Models (2023)
Amirata Ghorbani, James Zou. Data Shapley: Equitable Valuation of Data for Machine Learning (2019)
Ruoxi Jia, David Dao, Boxin Wang, Frances Ann Hubis, Nick Hynes, Nezihe Merve Gurel, Bo Li, Ce Zhang, Dawn Song, Costas Spanos. Towards Efficient Data Valuation Based on the Shapley Value (2019)
Pang Wei Koh, Percy Liang. Understanding Black-box Predictions via Influence Functions (2017)
Andrew Ilyas, Sung Min Park, Logan Engstrom, Guillaume Leclerc, Aleksander Madry. Datamodels: Predicting Predictions from Training Data (2022)